'Rope'

前言

学习deepseek的MLA(Multi-Head Latent Attention)时候，涉及到了rope（Rotary Position Embedding），之间只知道sin/cos绝对位置编码，所以决定弄清楚旋转位置编码的具体过程

为什么需要位置编码

Transformer架构的核心就是attention机制，而attention中的重点就是计算注意力分score，即Q K 矩阵的点积过程。我们可以很容易发现，改变token的顺序，并不会影响score的值，下面的代码可以快速验证这个过程：

import torch
x = torch.randn((3, 3))
x


def softmax(x):
    return torch.exp(x) / torch.exp(x).sum()


def attention(q, k, v):
    scores = (torch.matmul(q, k.transpose(-2, -1)) / q.size(-1) ** 0.5)
    scores = [
          softmax(row)  for row in scores
        ]
    scores = torch.stack(scores, dim=0)
    return torch.matmul(scores, v)

attn_x = attention(x, x, x) 
y = x[[1, 0, 2]] # 交换第一行和第二行
attn_y = attention(y, y, y) 

attn_x, attn_y
PYTHON

结果如下：

(tensor([[-0.1147, -1.8527, -1.4377],
         [ 0.4758, -2.0564, -1.7171],
         [ 0.5365,  0.4142,  0.4669]]),
 tensor([[ 0.4758, -2.0564, -1.7171],
         [-0.1147, -1.8527, -1.4377],
         [ 0.5365,  0.4142,  0.4669]]))
BASH

可以发现，score矩阵除了位置交换以外，对应的值没有改变。但是对于一个句子来说，词的顺序改变应该会引起句意的改变，所以我们需要引入位置信息到词嵌入向量，让token顺序的改变会引起score值的改变。

相对位置编码

现在假设有两token：$token_m, token_n$ ，通过函数 $f(token)$将位置信息加入到向量中，简写形式$f(m)$表示将 $token_m$ 加入位置信息m

我们的目的是找到一个合适的函数 $f$ 能够在做点积运算时，能够让结果与相对位置挂钩：

$$f(m) * f(n) = f(m - n)$$

同时，调换token顺序结果应该不同

$$f(m) * f(n) != f(n) * f(m)$$

很自然想到矩阵乘法不可逆，似乎可以将矩阵作为映射的权重，而旋转矩阵就是我们要找的矩阵。

旋转矩阵长下面这样：

$$R(\theta) = \left\{ \begin{matrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & sin(\theta) \\ \end{matrix} \right\}$$

他能够将二维向量逆时针旋转 $\theta$ ，即对于 $ V’ = R(\theta) V$ ，$V'$ 就是 $V$ 逆时针选择 $\theta$ 得到的向量

容易得到：

• $R(\alpha)^T = R(-\alpha)$
• $R(\alpha) * R(\beta) = R(\alpha + \beta)$

引入旋转矩阵，两向量$q_n^{rope}, k_m^{rope}$的点积过程如下：

$$q_n^{rope} = R(\alpha) q_n \\ \\ k_m^{rope} = R(\beta) k_m \\ \\ \begin{aligned}({q_n^{rope}})^T * k_m^{rope} &= (R(\alpha) q_n ) ^ T * R(\beta) k_m \\ &= q_n * R(-\alpha) * R(\beta) * k_m \\ &= q_n R(\beta - \alpha) k_m \end{aligned}$$

这里 $\alpha, \beta$ 与两个token的位置相对应，这样我们就能将结果与相对位置挂钩了。

扩展到多维（偶数）

image-20250329192007988

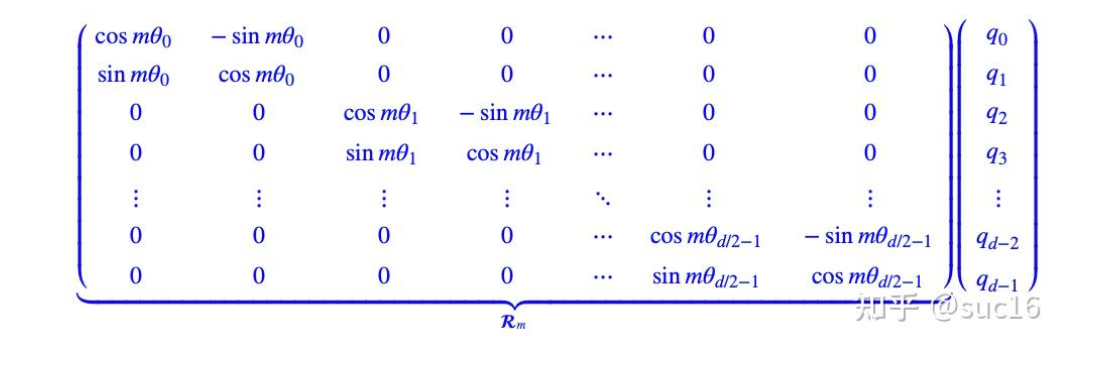
化简

image-20250329192026953

参考

LLM学习记录（五）–超简单的RoPE理解方式

旋转位置编码RoPE的简单理解